Curvas de Bézier

1. Introducción
2. Curva lineal o grado 1
3. Curva cuadrática o grado 2
4. Curva cúbica o grado 3
5. Curvas de mayor grado
6. Spline cúbico de Hermite
7. Notas
8. Referencias

Todo esto que voy a mencionar es lo que he aprendido de este tema que tiene uso práctico >:]

La interpolación es un procedimiento que se hace para generar puntos que conecten a 2 (o más) puntos determinados con la intención de tener algo útil que los conecte. Su contraparte, la extrapolación, es el procedimiento para generar puntos fuera de un intervalo de puntos y puede usarse para crear curvas que predigan el comportamiento de unos puntos base.

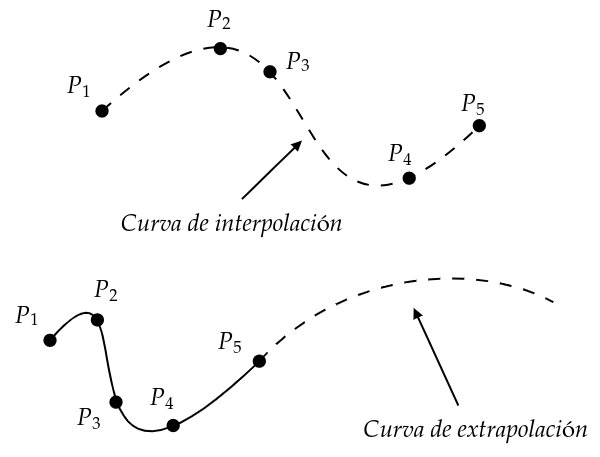
Las curvas de Bézier son un tipo de curva que se puede usar para hacer interpolación entre 2 puntos. La forma de la interpolación final depende del número de "puntos intermedios" que se usen. Estos puntos intermedios no son puntos por los cuales la curva va a pasar (puede que pase, pero ese no es el punto) sino puntos que rigen la forma que ésta va a tener en el espacio.

Dependiendo del número de puntos intermedios se tiene el grado de la curva de Bézier:

• 0 puntos intermedios --> Curva de Bézier lineal o grado 1.
• 1 punto intermedios --> Curva de Bézier cuadrática o grado 2.
• 2 puntos intermedios --> Curva de Bézier cúbica o grado 3.
• ...
• n puntos intermedios --> Curva de Bézier grado n+1

Al usar los 2 puntos extremos y los puntos intermedios definidos, lo que se busca es parametrizar cada coordenada en la que esten específicados los puntos en función de una variable. En este escrito se va a usar la letra t como esa variable.

Parametrizar consiste en especificar el comportamiento de una variable en función de otra. Esto agrega otros sistemas en el que cada variable se puede graficar en función de la variable de parametrización escogida.

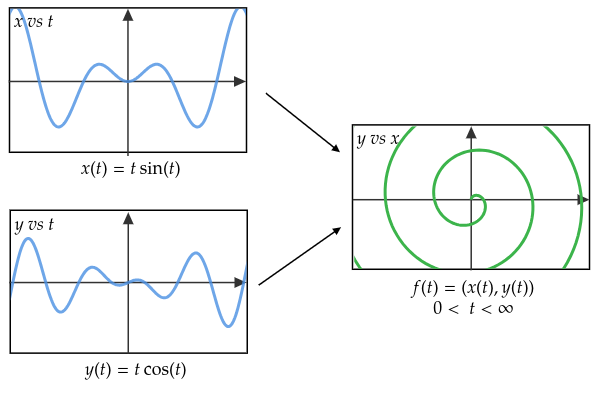
Ejemplo de una parametrización de 2 coordenadas. Con las parametrizaciones pueden generarse curvas poco usuales.

La interpolación que se hace entre 2 puntos sin puntos intermedios es la más básica: una recta que conecte a los puntos directamente.

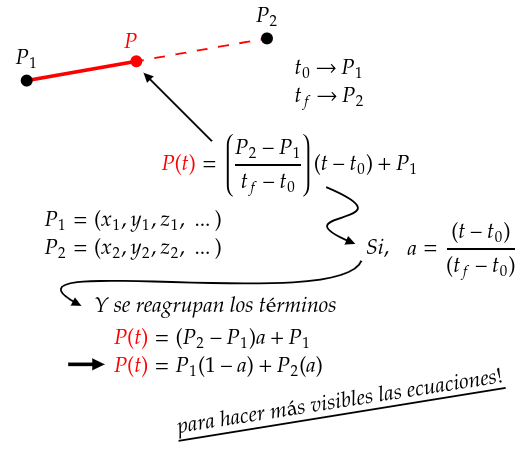
• El punto P es un punto genérico entre P1 y P2.
• La variable de parametrización t puede estar entre t0 y tf.
• El punto P1 corresponde a t0 y el punto P2 corresponde a tf.
• Los puntos pueden estar especificados de 1 dimensión en adelante. Es decir, pueden ser un valor numérico o algo que esté en más dimensiones.

El efecto de la curva de Bézier se ve mejor al interpolar puntos de 2 dimensiones por lo que los ejemplos de Desmos compartidos serán de esa forma. Desmos.

Imagen equivalente de Wikipedia.

Esta curva es la principal y a partir de ella se generan las demás.

La curva cuadrática se obtiene de la siguiente forma:

• Obtener las interpolaciones lineales entre los puntos P1 y P2, y P2 y P3.
• Obtener la interpolación entre un punto P12, que se encuentra en la interpolación lineal que se hizo entre P1 y P2, y un punto P23, que se encuentra en la interpolación lineal que se hizo entre P2 y P3.

Mejor hecho que dicho:

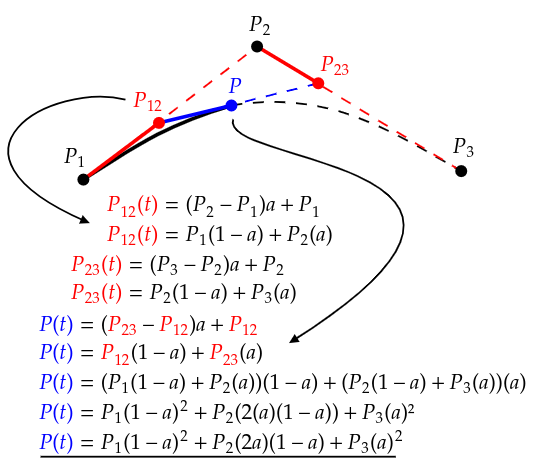
La expresión obtenida en la imagen corresponde a la de un polinomio de segundo grado (cuadrado), por eso el nombre de la curva es Bézier cuadrático. En la imagen se puede ver la curva generada (en negro) y como se genera al recorrer todas las interpolaciones lineales de principio a fin en "el mismo tiempo". Desmos.

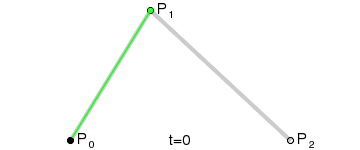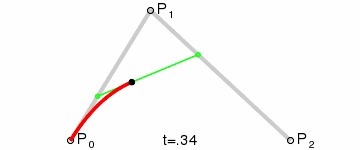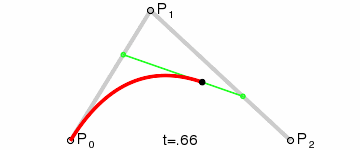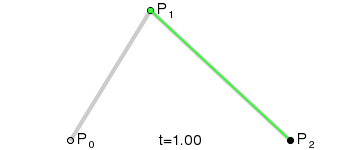
Imagen equivalente de Wikipedia.

La curva cúbica se obtiene de la siguiente forma:

• Obtener las interpolaciones lineales entre los puntos P1 y P2, P2 y P3, y P3 y P4.
• Obtener las interpolaciones lineales entre los puntos P12 y P23, y P23 y P34 generados en la primera interpolación.
• Obtener la interpolación lineal entre los puntos P123 y P234 generados en la segunda interpolación.

Aquí vamos otra vez:

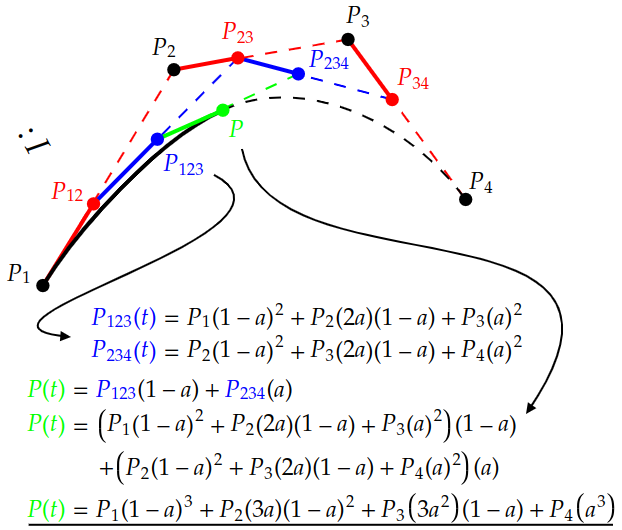
Las expresiones se van haciendo más largas... Desmos.

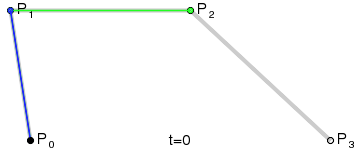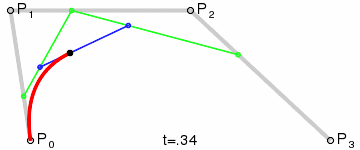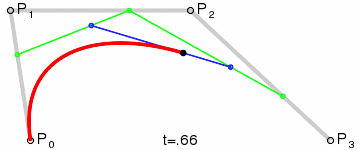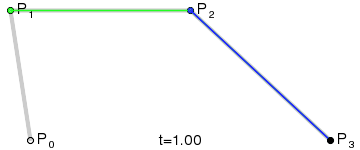
Imagen equivalente de Wikipedia.

Por lo mencionado arriba se puede más o menos predecir como construir las expresiones de grado n:

• Se hace interpolación lineal entre los puntos P_1 y P_2, P_2 y P_3 ..., P_(n-1) y P_(n), y, P_(n) y P_(n+1) (n interpolaciones).
• Se hace interpolación lineal entre los puntos P_12 y P_23, P_23 y P_34, ..., P_(n-2)(n-1) y P_(n-1)(n), y, P_(n-1)(n) y P_(n)(n+1) generados en la primera interpolación (n-1 interpolaciones).
• Se hace interpolación lineal entre los puntos P_123 y P_234, P_234 y P_345, ..., P_(n-3)(n-2)(n-1) y P_(n-2)(n-1)(n), y, P_(n-2)(n-1)(n) y P_(n-1)(n)(n+1) generados en la segunda interpolación (n-2 interpolaciones).
• ...
• Se hace interpolación lineal entre los puntos P_123...(n-2)(n-1) y P_234...(n-1)(n), y, P_234...(n-1)(n) y P_345...(n)(n+1) (2 interpolaciones).
• Se hace interpolación lineal entre los puntos P_123...(n-1)(n) y P_234...(n)(n+1) (1 interpolación).

Imágenes de Wikipedia.

Es un poco horrible pero pueden generarse las curvas de ese modo >:]

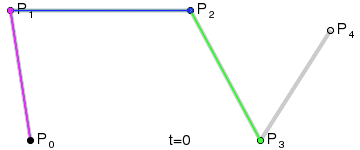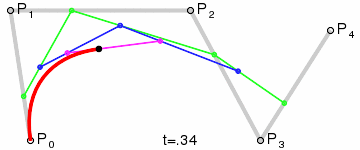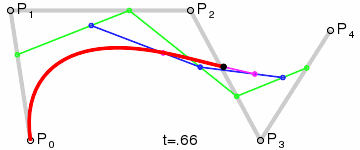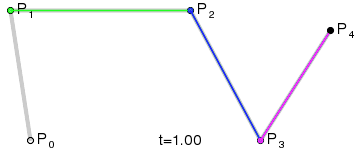
Este es un tipo de interpolador usado en la práctica y se puede especificar como una curva de Bézier cúbica. Su expresión general viene dada por

Visto desde la perspectiva de una curva de Bézier: En vez de especificar los valores de los 4 puntos necesarios para la interpolación de la curva (ya que es cúbica), especifica los puntos inicial y final de la interpolación (P0 y Pf), la "pendiente" para ir del primer punto al segundo (m0) y la "pendiente" para ir del tercero al último (mf). Estas pendientes no son respecto a la variable de parametrización t pero con respecto a la variable a.

Menciono esta expresión en este escrito ya que es el interpolador usado en las animaciones de esqueleto de Super Mario Galaxy. También, ya que tiene una peculiaridad, como se dijo, aquí no se especifica la posición de los puntos intermedios pero se especifica la pendiente, sin embargo, eso no me dice nada sobre la posición de esos puntos en la coordenada de interpolación y tampoco sobre el valor que tienen.

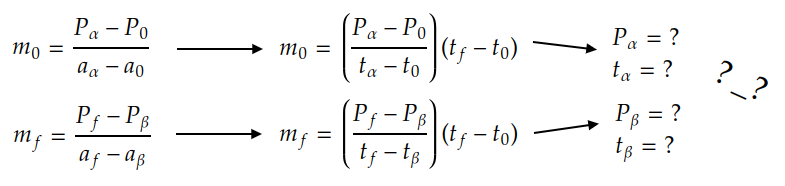
¿Cómo se puede saber en donde estan estos puntos en el sistema P vs t? Bueno, se me ocurrió usar una expresión Bézier cúbica 2D y empezar a asumir ciertas cosas...

• Se tiene un Spline cúbico de Hermite de 1D, P1(t1) = (y1(t1)), que va a graficarse en el sistema y1 vs t1. Esto ya que sólo hay puntos en una dimensión y quiero ver como la coordenada t1 se ajusta a los puntos y1.
• Se tiene una curva de Bézier cúbica 2D, P2(t2) = (x2(t2), y2(t2)), que se va a graficar en el sistema y2 vs x2.

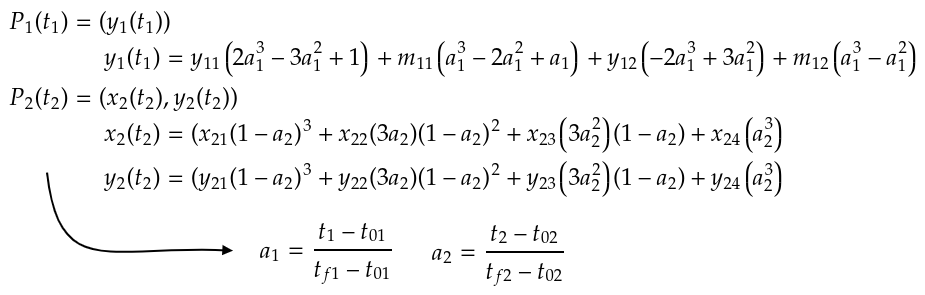
Como quiero ajustar la gráfica de y2 vs x2 a la que está en y1 vs t1 entonces y2(t2) = y1(t1) y x2(t2) = t1. Además, como y2(t2) = y1(t1) entonces t2 = t1 lo que implica que x2(t2) = t2. Por simplicidad en la notación, t2 = t1 = t, x2(t2) = t1 --> x(t) = t y y2(t2) = y1(t1) = y(t).

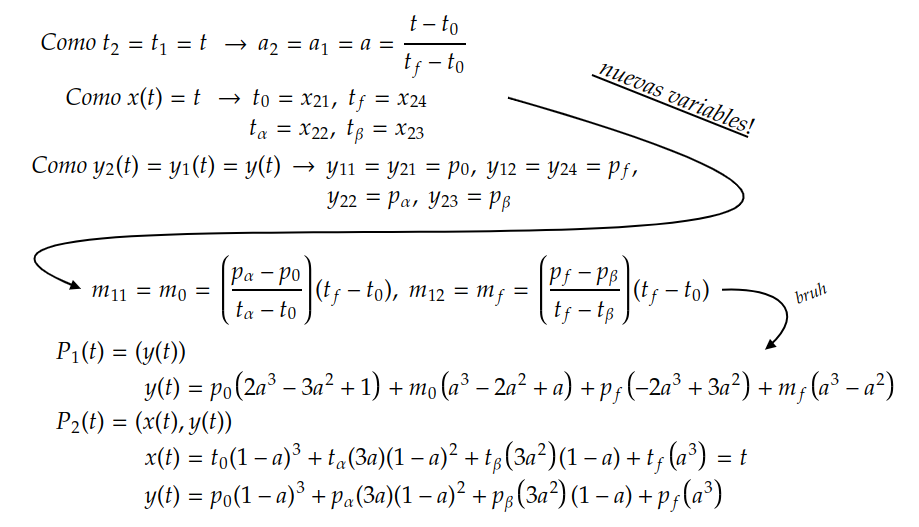
En la expresión de x(t) = t los puntos intermedios tα y tβ se asumen fijos (se supone que esos puntos no se mueven al cambiar la variable de parametrización). Considerando esto, se pueden generar varias expresiones x(t) = t con valores de t distintos en donde tα y tβ son variables. Todas las intersecciones entre las distintas x(t) = t deberían caer en un mismo punto entonces! Al hacer eso se reflejan los valores de tα y tβ que eran desconocidos (no quiero añadir la deducción general con sólo 2 rectas ya que es muy larga y fastidiosa así que solución gráfica a través de Desmos >:]).

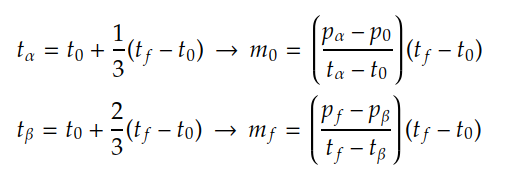
Como puede verse en el gráfico tα = t0 + (1/3)(tf - t0) y tβ = t0 + (2/3)(tf - t0). Esto significa que tα se ubica a 1/3 de la distancia entre t0 y tf, y tβ se ubica a 2/3 de la misma distancia. t0, tα, tβ y tf se encuentran igualmente espaciados entre sí!

Con esto ya se tienen todas las variables del Spline cúbico de Hermite desconocidas y cómo convertirlas para su uso en una curva de Bézier cúbica. Estoy seguro que hay otras formas de verificar esto de una forma más sencilla pero yo me compliqué moviéndome por aquí.

Spline cúbico de Hermite interactivo en Desmos

• Si t0 = 0 y tf = 1 entonces a = t.
• Los splines y las curvas de Bézier son cosas distintas (eso es lo que leí) pero en general se refieren a ellos como lo mismo ya que ambos se usan para interpolar y de ambos se pueden conseguir las mismas expresiones polinómicas.
• Es interesante notar que el Spline cúbico de Hermite sólo puede representar un rango de curvas de Bézier cúbicas 2D (las mismas pendientes pueden representar diferentes puntos en una curva de Bézier 2D). Esto es de esperarse ya que las posiciones de los puntos tα y tβ se asumen "ancladas", limitando grados de libertad.
• Respecto al Spline cúbico de Hermite: De cierta forma (y esto lo puedo decir después de todo lo dicho anteriormente) es predecible que los puntos en la variable de parametrización se encuentren igualmente espaciados entre sí ya que la variable aumenta linealmente. En la práctica esta expresión se usa como el tiempo en animaciones.
• Me parece que "SPLine" significa: Soft Polynomial Line >:]

• Bézier curve
• Cubic Hermite Spline