Rotaciones

1. Introducción a las rotaciones
2. Rotaciones activas y pasivas
3. Ángulos de Euler
4. Rotaciones intrínsecas
5. Rotaciones extrínsecas
6. Relación entre la rotación intrínseca y extrínseca
7. Referencias

Las rotaciones, en mi opinion, son uno de los temas más interesantes en los que se pueden aplicar las matrices y la geometría. Manejar esta teoría hace sentir que uno tiene cierto grado de dominio de la realidad que uno vé >:] Para empezar a caracterizar esta operación de naturaleza geométrica es necesario el uso de ejemplo visuales.

A continuación se muestra un sistema de referencia S bidimensional de ejes coordenados 1 y 2.

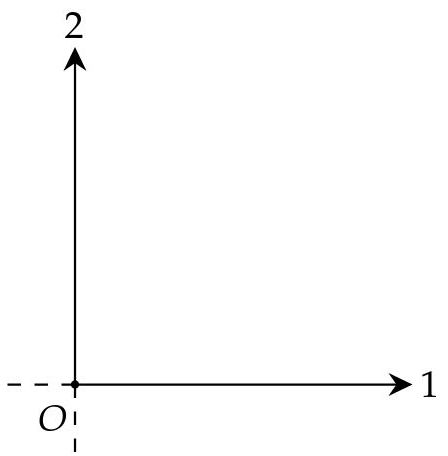
Fig. 1: Sistema de referencia S con ejes coordenados 1 y 2.

Quiero crear un sistema S^ que esté rotado un angulo θ en sentido antihorario respecto al sistema S.

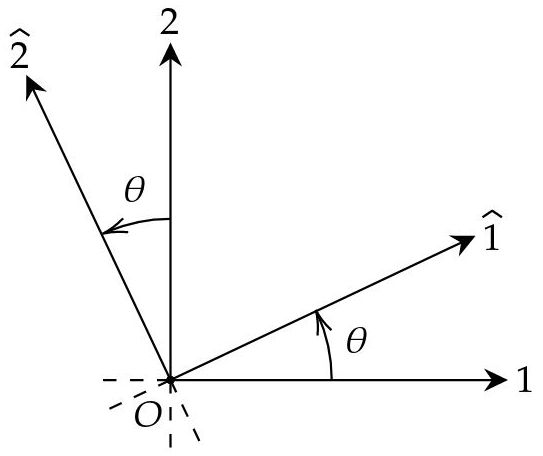
Fig. 2: Sistema de referencia S^ con ejes coordenados 1^ y 2^.

Si se intentan proyectar los vectores del sistema S^ sobre los del sistema S se obtienen las siguientes ecuaciones

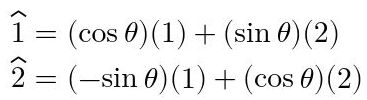
Fig. 3: Vectores del sistema S^ proyectados sobre el sistema S.

a partir de las cuales se puede formar el siguiente arreglo matricial.

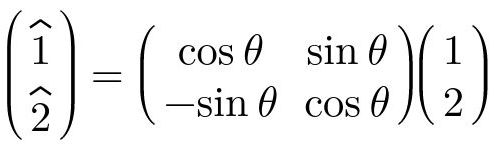
Fig. 4: Ecuaciones del sistema de la Fig. 3 escritas en un arreglo matricial.

El sistema de la Fig. 4 contiene una matriz de 2x2 (denominada matriz de coeficientes) que transforma (en este caso) los vectores 1 y 2 del sistema S en los vectores 1^ y 2^ del sistema S^. Con símbolos, la matriz A de la figura puede hacer la transformación de elementos S→S^. Esta misma matriz puede usarse para transformar puntos o vectores. Por ejemplo, el vector de S v = (0, 1) es proyectado al sistema S^ como el vector v^ = (sinθ, cosθ). En la siguiente imagen puede verse dicha transformación.

Nota: El sistema matricial de la Fig. 4 no es usual ya que los elementos 1, 2, 1^ y 2^ no son escalares sino vectores.

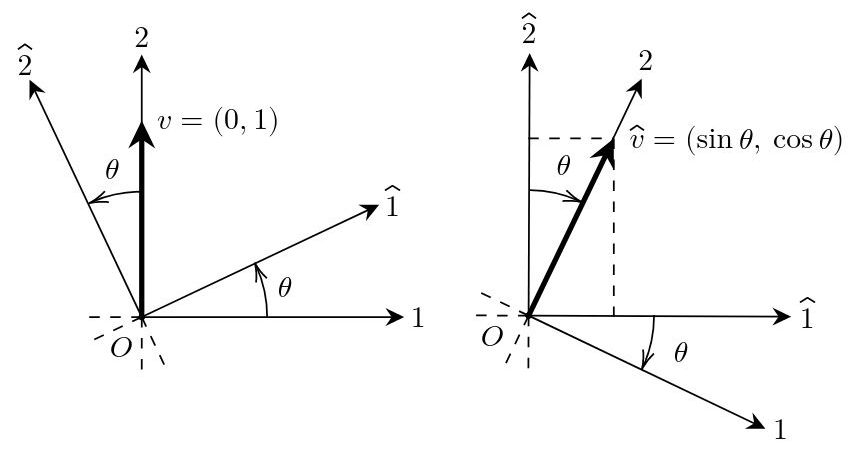
Fig. 5: Transformación del vector de S, v = (0, 1), al sistema S^.

Más allá de un simple cambio de sistema, veamos lo que le hace esta matriz a un vector de S si el vector resultante se forza a ser escrito en el mismo sistema de origen S.

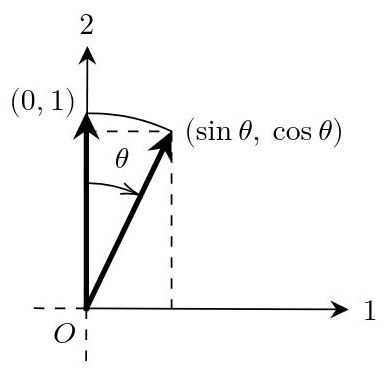
Fig. 6: Transformación del vector de S, v = (0, 1), representado en el sistema S.

El vector resultante está rotado θ grados del vector original.

Con lo mostrado, se puede ver que la matriz de rotación A tiene 2 significados distintos dependiendo del contexto en el que se esté usando:

• En primer lugar: Determina la existencia de un sistema de coordenadas S^ que parte del sistema S que puede verse como un sistema S rotado un ángulo θ (sentido antihorario) al que pueden proyectarse los elementos del sistema S original (sin transformaciones).
• En segundo lugar: Crea un elemento, a partir de un elemento de S, que representado en S se encuentra rotado en un ángulo θ (sentido horario) respecto al elemento original.

Estas 2 propiedades dan pie a las definiciones de rotación pasiva y rotación activa respectivamente.

Adicionalmente, se tienen las siguientes propiedades de las matrices de rotación:

• La inversa de una matriz de rotación representa la rotación opuesta, es decir, si una matriz de rotación define una rotación en θ entonces la inversa define una rotación en -θ

• Se puede generar una matriz de rotación que represente la aplicación de diversas matrices de rotación simples como sigue (en orden)

  

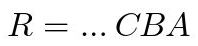
  Fig. 6: Producto de matrices de rotación.

  Esto se lee:

  • Se comienza con la rotación A
  • Después de la rotación A se aplica la rotación B (opera a la izquierda de A)
  • Después de la rotación B se aplica la rotación C (opera a la izquierda de B)
  • ...

  De esta forma pueden encadenarse rotaciones para entonces generar una matriz de rotación final R que puede aplicarse (por la izquierda) al elemento que se quiere transformar.

De la sección anterior pudo verse que la matriz de rotación A tiene 2 significados dependiendo del contexto. Esos usos describen las rotaciones pasivas y las rotaciones activas. Si se tiene un sistema de referencia S y elementos pertenecientes a S:

• Las rotación pasiva consiste en transformar los elementos de un sistema S al crear un sistema secundario S^ a partir del cual dichos elementos se ven rotados. Rota indirectamente los elementos de S ya que la rotación es aplicada al observador (sistema de referencia) y no a los elementos.
• Las rotación activa, en cambio, consiste en transformar los elementos de un sistema S modificando la posición de dichos elementos directamente. Activamente se estan transformando los elementos para ubicarse de forma diferente bajo el mismo sistema S.

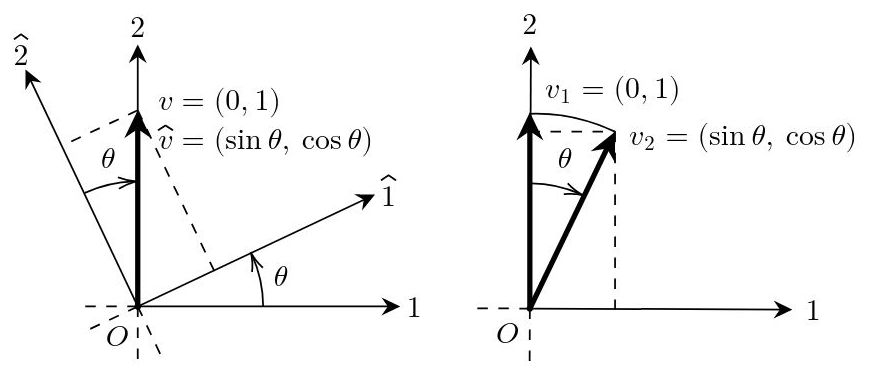
Fig. 7: Rotación pasiva (izquierda) vs activa (derecha).

Los ángulos de Euler (pronunciado en español como Oiler) son un conjunto de 3 ángulos que sirven para describir cualquier dirección en un sistema de coordenadas tridimensional. Fueron desarrollados por Leonhard Euler para describir el movimiento de rotación de sólidos rígidos.

Hasta el momento conozco de 2 implementaciones de dichos ángulos, una usada para descripciones de movimientos de cuerpos en física y otra usada para programas de modelado 3D. Estas son, las rotaciones intrínsecas y las rotaciones extrínsecas.

Las rotaciones intrínsecas son un tipo de rotación en el que los ejes a través de los cuales se hacen las rotaciones van transformándose a medida que se aplican las rotaciones. Es decir, ocurre una primera rotación y la siguiente ocurre en un eje que fue afectado por la rotación anterior.

Vamos a visualizar el proceso, rotación por rotación. Se usará la notación de sistemas de referencia implementada por el Prof. Desloge en su libro Classical Mechanics citado en las referencias.

Primero, se tiene el siguiente sistema de referencia tridimensional S de ejes perpendiculares 1, 2 y 3.

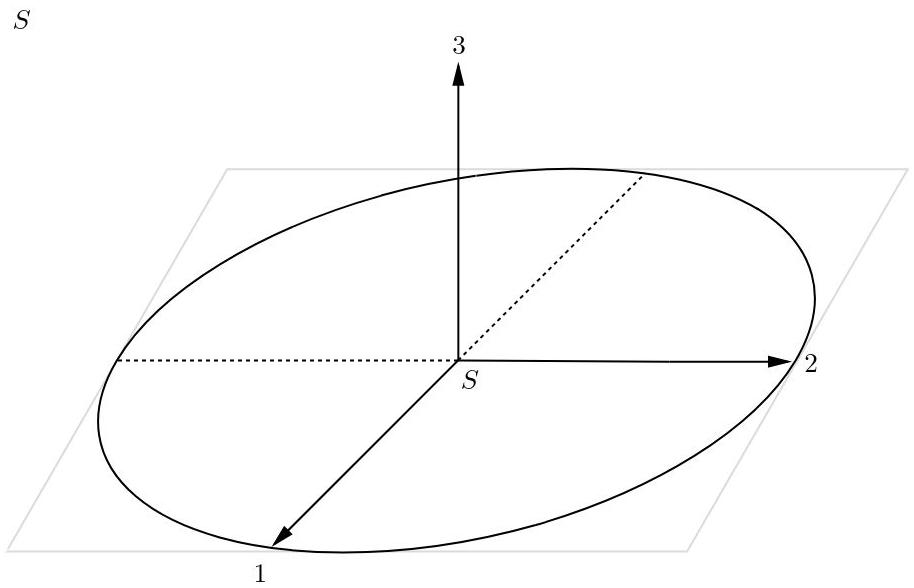
Fig. 8: Sistema de referencia S con sus ejes perpendiculares.

Se realiza la primera rotación alrededor del eje 3 y se genera el sistema S^ con ejes perpendiculares 1^, 2^ y 3^. Como la rotación se realiza respecto al eje 3 entonces los ejes 3 y 3^ se encuentran uno sobre el otro.

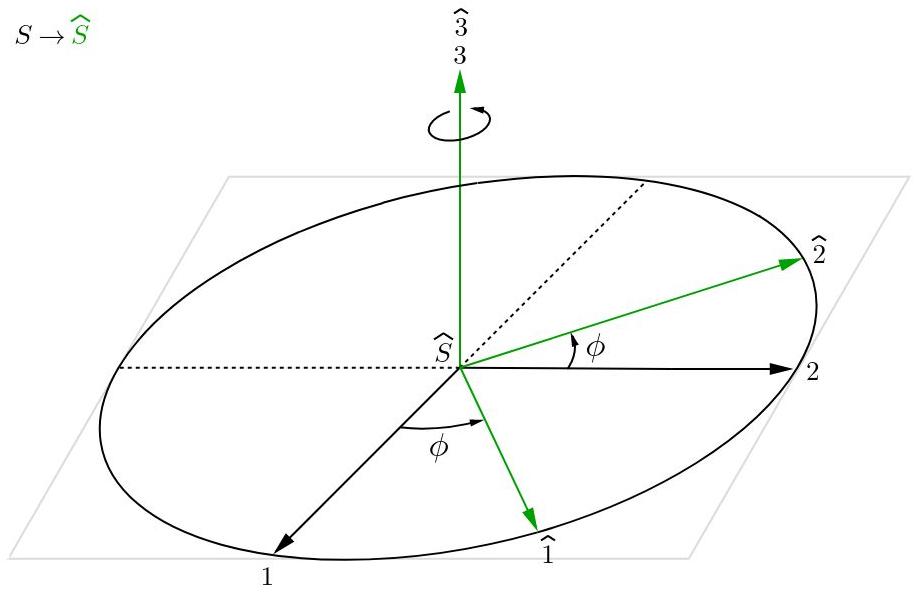
Fig. 9: Sistema de referencia S^ con sus ejes perpendiculares (verde).

A partir de la imagen, se puede obtener la matriz de transformación S→S^ proyectando los vectores de S^ en S como sigue.

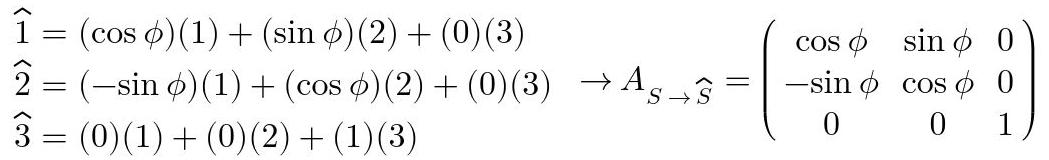
Fig. 10: Obtención de la matriz de transformación S→S^

Se realiza la segunda rotación alrededor del eje 1^ y se genera el sistema S˜ con ejes perpendiculares 1˜, 2˜ y 3˜. Como la rotación se realiza respecto al eje 1^ entonces los ejes 1^ y 1˜ se encuentran uno sobre el otro.

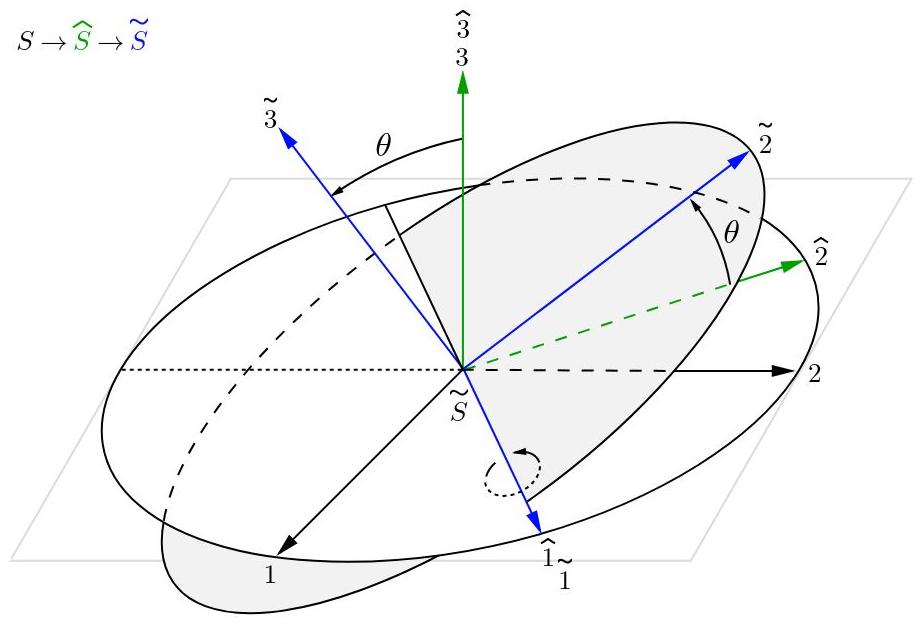
Fig. 11: Sistema de referencia S˜ con sus ejes perpendiculares (azul).

A partir de la imagen, se puede obtener la matriz de transformación S^→S˜ proyectando los vectores de S˜ en S^ como sigue.

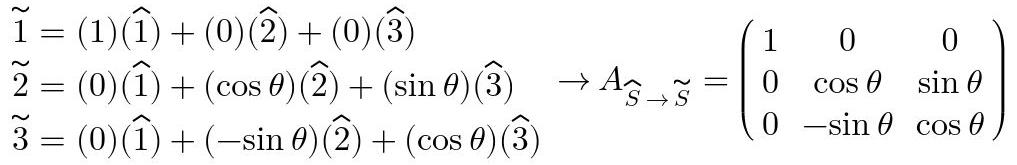
Fig. 12: Obtención de la matriz de transformación S^→S˜

Se realiza la tercera rotación alrededor del eje 3˜ y se genera el sistema S‾ con ejes perpendiculares 1‾, 2‾ y 3‾. Como la rotación se realiza respecto al eje 3˜ entonces los ejes 3˜ y 3‾ se encuentran uno sobre el otro.

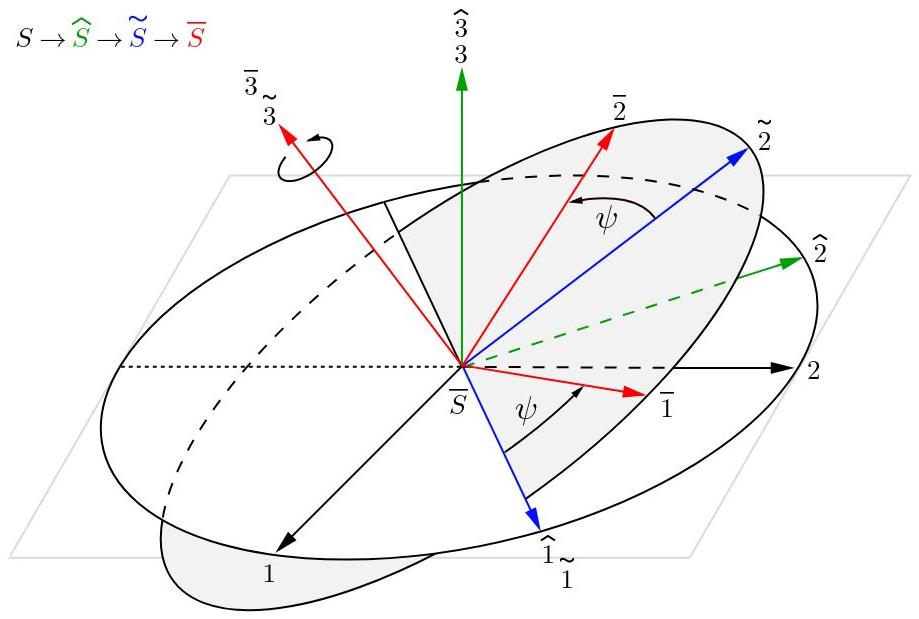
Fig. 13: Sistema de referencia S‾ con sus ejes perpendiculares (rojo).

A partir de la imagen, se puede obtener la matriz de transformación S˜→S‾ proyectando los vectores de S‾ en S˜ como sigue.

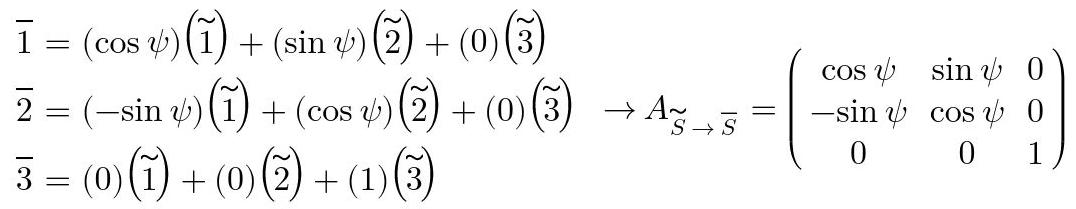
Fig. 14: Obtención de la matriz de transformación S˜→S‾

Con las matrices de coeficientes de las Figs. 10, 12 y 14 se puede generar una sola matriz que abarque las 3 rotaciones y sirva entonces para proyectar un vector de S directamente en S‾.

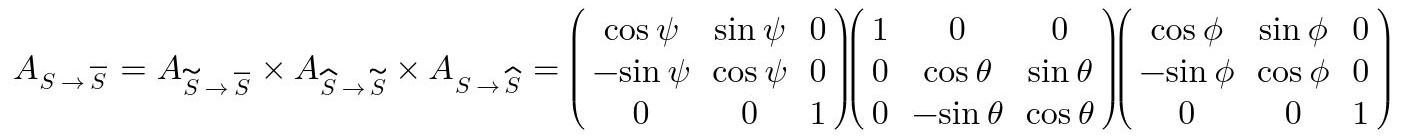
Fig. 15: Obtención de la matriz de transformación S→S‾

Como al final lo que se quiere es rotar un elemento en los angulos φ, θ y ψ mostrados en las imagenes, y por lo concluido al final de la primera sección de la página, la matriz de rotación que rotará un elemento en S bajo el sistema de rotación intrínseco mostrado en las figuras es:

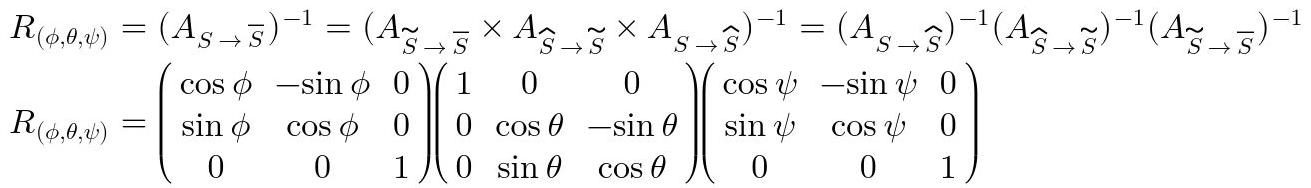
Fig. 16: Obtención de la matriz de rotación intrínsica en 3 dimensiones.

Nota: Las matrices de rotación obtenidas son ortogonales.

---

Video ilustrando cada rotación en el proceso de rotación intrínseca explicado (hecho en Blender 2.79)

Vid. 1: Video ilustrativo del proceso de rotación intrínseca.

---

En las figuras anteriores se ilustró la rotación intrínseca tridimensional, sin embargo, no se explicó el porqué de la elección de cada eje para realizar cada rotación. Bueno, no puedo explicar el porqué pero si puedo decir que los ejes de rotación a escoger están definidos de la siguiente forma:

1. Se selecciona un eje del sistema S (cualquiera entre 1, 2 y 3).
2. Luego, se selecciona un eje del sistema S^ que sea diferente en número del que se escogió para la primera rotación. Es decir, si se escogió el eje 3 para la primera rotación, se puede seleccionar entre los ejes 1^ o 2^ para realizar la segunda rotación.
3. Finalmente, para la tercera rotación, se selecciona el eje del sistema S˜ que posea el mismo número que el eje que se escogió para la primera rotación. Es decir, si se seleccionó el eje 3 para la primera rotación, en la tercera rotación se tiene que escoger al eje 3˜.

Las reglas de escogencia mencionadas tienen el propósito de permitir que el movimiento de rotación realmente pueda describir cualquier dirección en el espacio 3D. Si se escogen los ejes de rotación arbitrariamente entonces se tiene el riesgo de "perder grados de libertad" en el proceso. Con estas reglas, las rotaciones intrínsecas tienen diferentes variaciones, la explicada en esta página es el tipo de rotación 3→1^→3˜ (o 313 para ser más coloquial) pero puede existir la rotación 2→1^→2˜, 3→2^→3˜, 1→2^→1˜, etc.

Las rotaciones extrínsecas, en contraste con las intrínsecas, son un tipo de rotación en el que los ejes de rotación a utilizar son todos de un mismo sistema de referencia, el sistema base S.

Vamos a ver cada rotación individual, se usará la misma notación que se usó en la sección anterior.

Como las rotaciones se hacen desde un solo sistema de referencia y se deben hacer 3 rotaciones (por los 3 ángulos de Euler) entoces se debe hacer una rotación en cada eje del sistema S, como sigue

---

Rotación a lo largo del eje 1

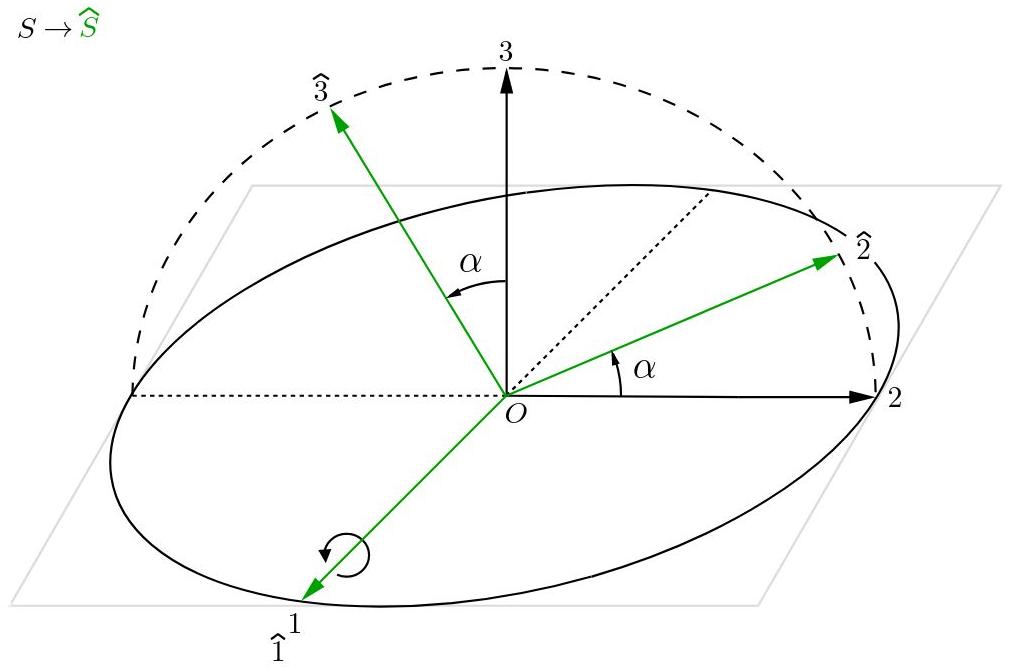
Fig. 17: Rotación alrededor del eje 1.

Al proyectar los vectores del sistema S^ sobre el sistema S se obtiene la siguiente matriz de transformación:

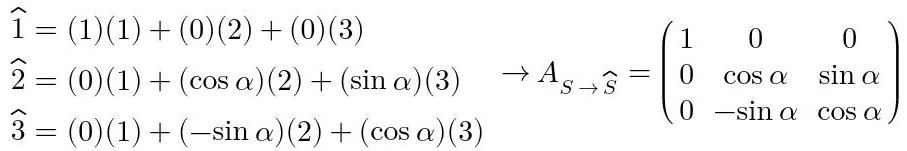
Fig. 18: Obtención de la matriz S→S^.

---

Rotación a lo largo del eje 2

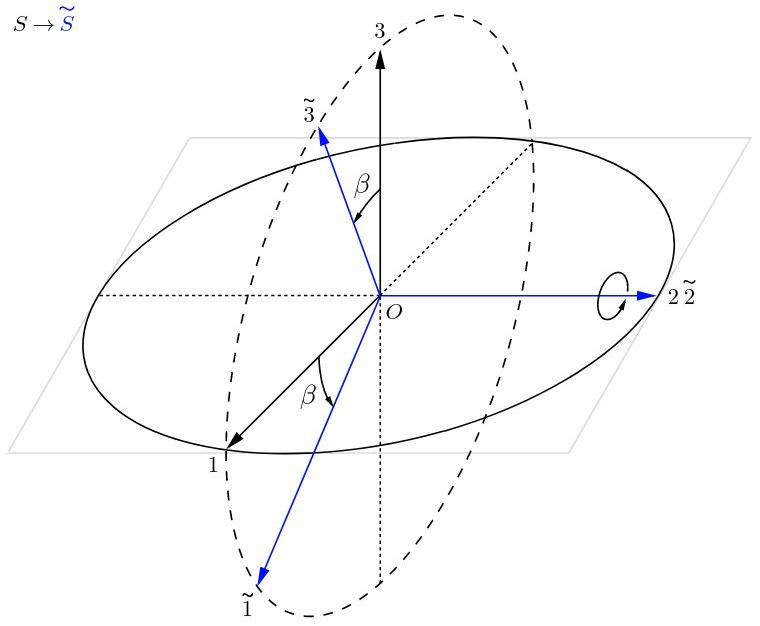
Fig. 19: Rotación alrededor del eje 2.

Al proyectar los vectores del sistema S˜ sobre el sistema S se obtiene la siguiente matriz de transformación:

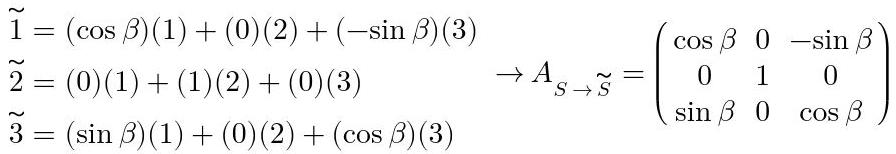
Fig. 20: Obtención de la matriz S→S˜.

---

Rotación a lo largo del eje 3

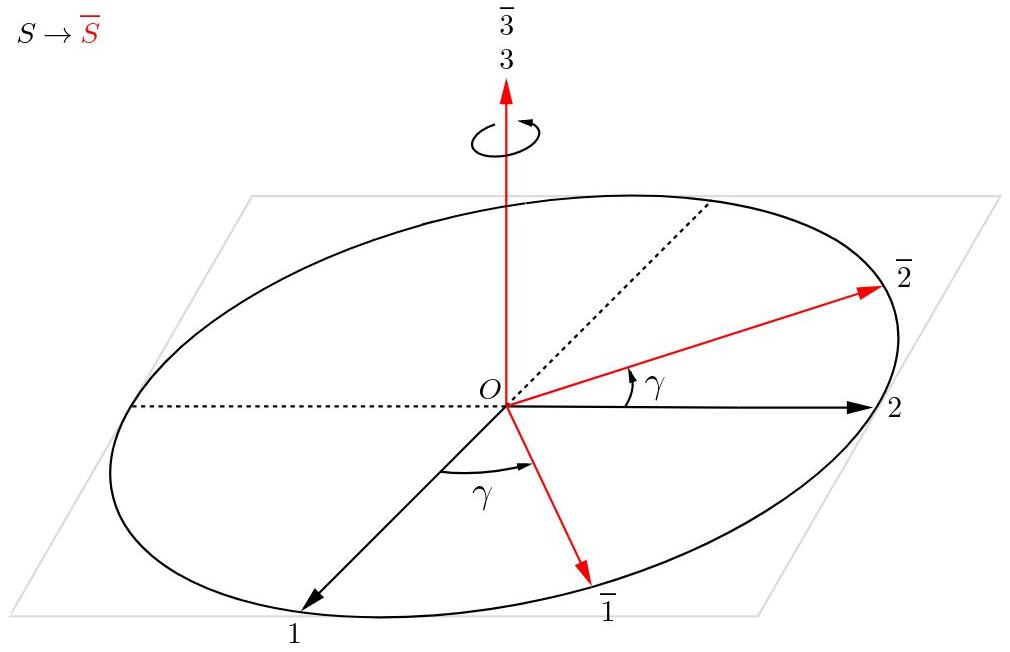
Fig. 21: Rotación alrededor del eje 3.

Al proyectar los vectores del sistema S‾ sobre el sistema S se obtiene la siguiente matriz de transformación:

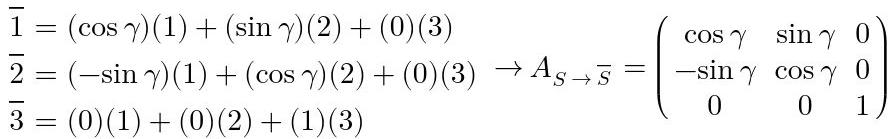
Fig. 20: Obtención de la matriz S→S‾.

---

Por lo concluido en la primera sección de esta página, las matrices de rotación activa respectivas son:

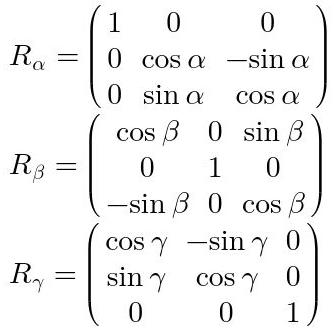
Fig. 21: Matrices de rotación extrínsecas R.

Estas matrices se pueden aplicar en el orden deseado dando lugar a diferentes variaciones de sistemas de rotación extrínsecos. El sistema usual usado en Blender 2.79 (programa de modelado 3D) es uno extrínseco denominado Euler XYZ. Lo que esto significa es que las matrices de rotación extrínsecas obtenidas se aplican en el orden 123, es decir, primero la matriz de rotación en 1, luego la matriz de rotación en 2 y por último la matriz de rotación en 3.

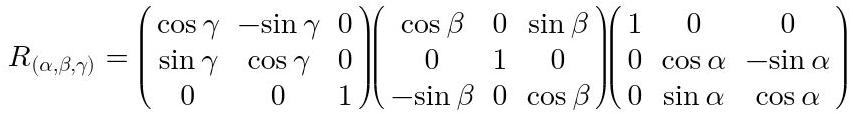
Fig. 22: Matriz de rotación extrínseca 123.

---

Video ilustrando cada rotación en el proceso de rotación extrínseca explicado (hecho en Blender 2.79)

Vid. 2: Video ilustrativo del proceso de rotación extrínseca.

---

Después de haber leído las 2 secciones anteriores, te podrás preguntar, ¿Porqué no se usa nada más la rotación extrínseca que es mucho más fácil de ver? No es por lo fácil de su usar/entender, es por el uso que se le va a dar. Las rotaciones intrínsecas sirven para simplificar enormemente calculos físicos orientados a centros de masa y momentos de inercia (se usa mayormente para aplicar rotaciones a sistemas de referencia) ya que se cambia el sistema de referencia desde el cual se miden dichas características, y las extrínsecas son solo las rotaciones absolutas respecto a un sistema de coordenadas (se usa mayormente para aplicar rotaciones a elementos de un sistema) que ayudan enormemente en el proceso de modelado 3D.

Esto no significa que ambos métodos de rotación son completamente diferentes, en absoluto, una rotación intrínseca se puede escribir como una rotación extrínseca y viceversa. Los angulos entre rotaciones son diferentes ya que se refieren a distintos sistemas de coordenadas. La primera rotación intrínseca es igual (en naturaleza) a la primera rotación extrínseca, ya a partir de la segunda rotación las cosas son diferentes.

• Classical Mechanics, Volume 1, Edward A. Desloge
• https://es.wikipedia.org/wiki/%C3%81ngulos_de_Euler
• https://es.wikipedia.org/wiki/Transformaci%C3%B3n_activa_y_pasiva