Contenido
- Introducción a las matrices
- Operaciones básicas con matrices
- Matrices traspuestas
- Sistemas de ecuaciones lineales
- Método de eliminación de Gauss-Jordan
- Matrices triangulares, diagonales y escalares
- Matrices cuadradas
- Matrices unidad/identidad
- Menor complementario
ijde una matriz - Cofactor
ijde una matriz - Determinante de una matriz cuadrada
- Inversa de una matriz cuadrada
- Matrices ortogonales
- Referencias
Introducción a las matrices
Esta página no trata de reemplazar todo el material asociado con las matrices, es sólo una simple introducción para poder trabajar con matrices lo más rápido posible. La mejor forma de aprender a usarlas es aprendiendo de un buen curso de algebra lineal.
Las matrices se mencionan mucho y se ven bastante intimidantes, pero como todo elemento matemático, es una entidad definida para trabajar con números de una forma especial a través de operaciones específicas y también definidas. En la imagen se puede ver la forma básica de una matriz.

Fig. 1: Imagen de una matriz
En la imagen puede verse una matriz de 3 filas y 4 columnas llena de números enteros. Las matrices son básicamente eso, son mallas cuadriculadas en donde cada cuadrado es un espacio reservado para un número de cualquier tipo (natural, entero, racional, irracional, real, imaginario...) ¿Qué significa esta matriz, o qué se hace con lo que está adentro de ella? Ni idea, eso ya depende del que la creó.
En general las matrices de tamaño m x n se representan de la siguiente forma:

Fig. 2: Imagen de una matriz general
donde cada elemento tiene un índice genérico ij que indica en que fila (i) y columna (j) se encuentra dicho elemento. Finalmente, las matrices tienen las siguientes restricciones:
- Las matrices tienen una forma rectangular, es decir, si la matriz tiene tamaño
3x4entonces la matriz tiene 12 casillas para rellenar. - Todas las casillas de la matriz deben contener elementos definidos (no pueden haber casillas vacias).
Operaciones básicas con matrices
Como los números, las matrices tienen las siguientes propiedades/operaciones definidas:
-
Suma de matrices: la suma de matrices se define como la suma del elemento ij de una matriz con el elemento ij de la otra matriz.
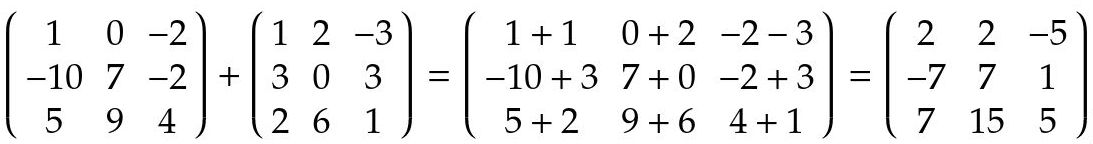
Fig. 3: Suma de matrices
Es ilegal sumar matrices que no tengan el mismo número de filas o columnas.
Resta de matrices: la resta de matrices sigue la misma regla que la suma solo que en vez de sumar los elementos, se restan.
-
Escalar multiplicando a una matriz: un escalar (un número) puede multiplicar a una matriz y lo que hace es multiplicar cada elemento
ijde la matriz por dicho escalar.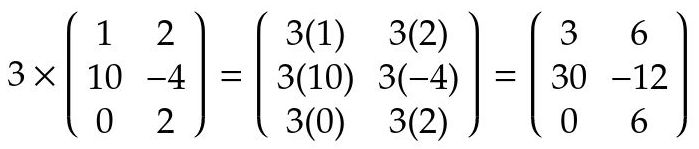
Fig. 4: producto de un escalar por una matriz
-
Multiplicación de matrices: esta es la operación más extraña y la más usada de las matrices. Dicha operación no es commutativa (importa el order) y sólo es legal cuando la matriz de la izquierda tiene un número de columnas igual al número de filas de la matriz de la derecha.
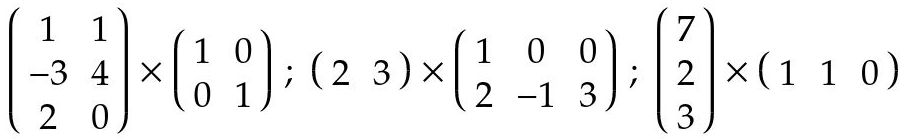
Fig. 5: matrices que pueden multiplicarse
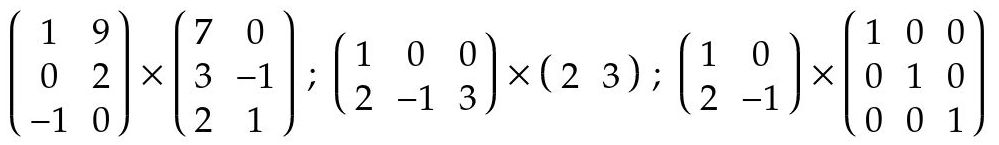
Fig. 6: matrices que NO pueden multiplicarse
Dicho de otra forma, si se tiene una matriz
Adem x py una matrizBdeq x nentonces la multiplicaciónA x Bsolo está definida para cuandop = q. El procedimiento para generar el elementoijde la matrizCque es el producto de las matricesA x Bes el siguiente:-
Se selecciona la fila
ide la matriz de la izquierdaA.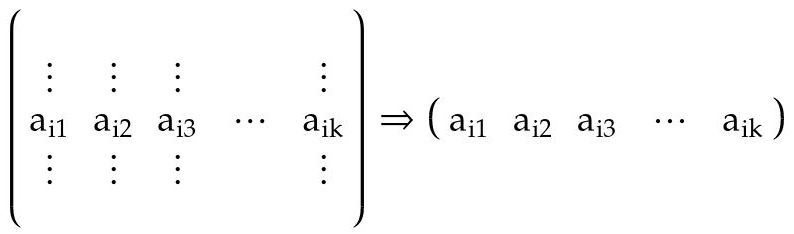
Fig. 7: fila
ide la matrizA -
Se selecciona la columna
jde la matriz de la izquieraB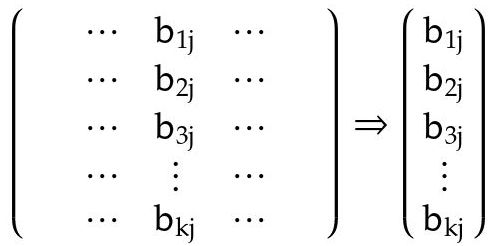
Fig. 8: columna
jde la matrizB -
Se multiplica cada elemento de la fila
ideAcon el elemento correspondiente de la columnajdeB(izquierda-derecha corresponde a arriba-abajo) y se suman todos los productos. Es como el producto escalar de vectores.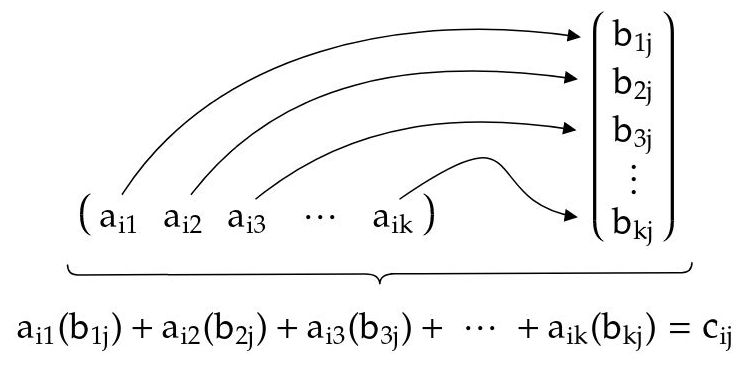
Fig. 9: "producto escalar" de la fila
ide la matrizAcon la columnajde la matrizB -
El resultado numérico es el elemento
ijde la matrizCresultante.
Para generar a la matriz completa solo hay que repetir este proceso multiples veces. Para cada fila de la matriz de la izquiera se hace la operación mencionada con cada columna de la matriz de la derecha para ir generando cada fila de la matriz resultante.
Ejemplos:
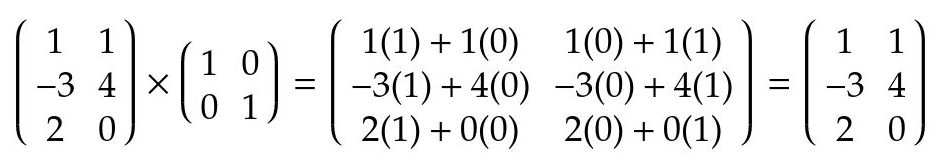
Fig. 10: ejemplo de producto de matrices
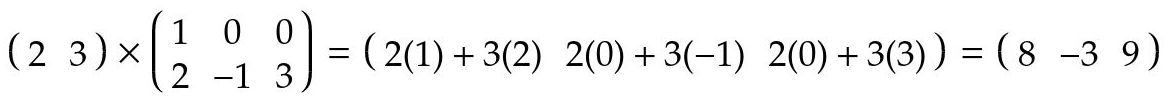
Fig. 11: ejemplo de producto de matrices

Fig. 12: ejemplo de producto de matrices
-
Matrices traspuestas
La trasposición es una operación que se realiza sobre las matrices y que lo único que hace es colocar las filas de la matriz como las columnas en la matriz resultante. Se usa el símbolo de elevado a la T para indicar que se quiere la traspuesta de una matriz.
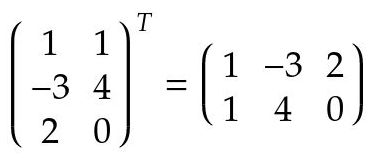
Fig. 13: Matriz traspuesta de una matriz
El orden de selección de las filas es de arriba a abajo y el del posicionamiento de las columnas de izquierda a derecha. De una forma más técnica se dice que la operación de trasposición lo que hace es agarrar el elemento ij de una matriz A y colocarlo en la posición ji de la matriz B. Esta operación tiene propiedades que se pueden ver en las referencias citadas.
Sistemas de ecuaciones lineales
En el material que aprendí, las matrices se empiezan a explicar a través de su aplicación en los sistemas de ecuaciones lineales. Para mí, le da a las matrices una razón de existencia (aunque no sé cual es el verdadero origen). El material expuesto en esta página empieza ligeramente al revés.
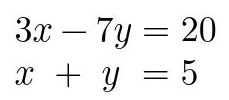
Fig. 14: Imagen de un sistema de ecuaciones lineal de 2 ecuaciones con 2 incognitas
¿Porqué hablar de los sistemas de equaciones lineales? Bueno, hay una propiedad fundamental de las matrices que "naturalmente" se explica a través de ellos por lo que es muy importante entender la aplicación. Voy a asumir que el lector ya sabe de estos sistemas, su interpretación geométrica (cuando puede aplicarse) y sus métodos de resolución.
Viendo la imagen de la Fig. 14 se puede comparar la posición de los escalares que multiplican a las incognitas x y y como las posiciones que tendrían en una matriz, vamos a ponerlos en una matriz entonces!
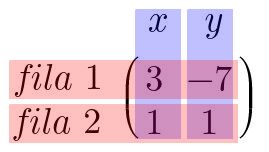
Fig. 15: Escalares del sistema de la Fig. 14 puestos en una matriz.
En la imagen puede verse que colocar a los números en una matriz permite contener casi toda la información del sistema de ecuaciones anterior recordando que cada columna corresponde a una de las incognitas del sistema y que la información de una ecuación se encuentra en una de las filas. Para incluir el resto de la información solo se incluye una columna extra con los elementos a la derecha de la igualdad del sistema.
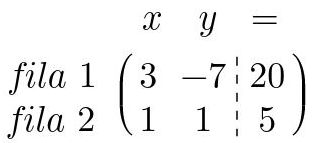
Fig. 16: Todos los escalares del sistema de la Fig. 14 puestos en una matriz.
Al tipo de matriz mostrada en la Fig. 15 se le conoce como matriz de coeficientes y a la matriz de la Fig. 16 se le denomina matriz aumentada/extendida. La extensión se puede representar con una línea. La distinción entre la matriz de coeficientes (sin la columna de extensión) y la matriz aumentada es que se pueden realizar operaciones en una matriz o en la otra para caracterizar/resolver al sistema de ecuaciones asociado, por lo que ambas representaciones son importantes.
Método de eliminación de Gauss-Jordan
Para resolver sistemas de ecuaciones se puede emplear los métodos de reducción, sustitución, etc. conocidos que trabajan directamente sobre las ecuaciones. En forma de matriz extendida, sin embargo, se puede emplear el método de eliminación de Gauss-Jordan.
Este método permite operar directamente en la matriz extendida (el método puede operarse sobre cualquier matriz) modificandola por pasos hasta obtener la solución del sistema de equaciones (si es que existe). Antes de explicar el método, veamos un ejemplo del inicio y el final del proceso de solución de un sistema de ecuaciones:
El sistema de ecuaciones mostrado en la Fig. 14 tiene la siguiente solución (solución única).
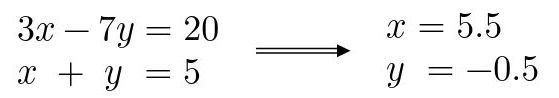
Fig. 17: Sistema de ecuaciones de la Fig. 14 con su solución.
Realmente, ambos elementos en la imagen de arriba son sistemas de ecuaciones, lo que pasa es que uno ya está resuelto (derecha, x y y están despejados) y el otro está por resolverse (izquierda). Por lo tanto, ambos pueden representarse como una matriz extendida.

Fig. 18: Sistemas de ecuaciones de la Fig. 17 en su forma de matriz extendida.
¿Porqué se representa la parte derecha de la Fig. 17 en la forma de matriz extendida de esa forma? la primera ecuación x = 5.5 tiene al escalar 1 multiplicando a la x y el escalar 0 multiplicando a la y (por ello no se coloca en la ecuación aunque no estaría mal colocarlo), la misma lógica aplica a la ecuación y = -0.5.
El método de Gauss-Jordan justamente tiene como inicio y final las matrices izquierda y derecha de la Fig. 18 y las operaciones intermedias definidas (y como representarlas al usarlas) son las siguientes:
-
Intercambiar filas de posición
Como lo dice el nombre, simplemente se intercambian las filas de lugar y se continua con el proceso.
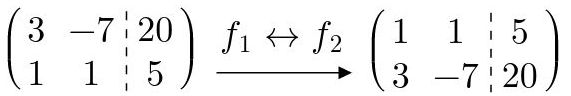
Fig. 19: Intercambio de filas.
Nota: Tambien pueden intercambiarse las columnas pero hay que tener en cuenta (además) la ubicación de las columnas para ubicar correctamente las incognitas.
-
Multiplicar una fila por un escalar
Se asigna a una fila el valor de la fila multiplicada por un escalar.
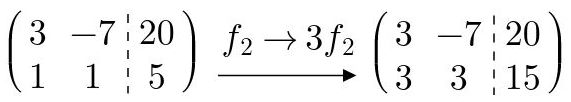
Fig. 20: Multiplicar fila por un escalar.
-
Asignar a una fila la combinación lineal de ella misma con otra fila
Esta es la operación más usada (y puede ser la única a usar) para el método de Gauss-Jordan. Basicamente es asignar a una fila en específico un multiplo de ella misma sumado con un multiplo de otra fila.
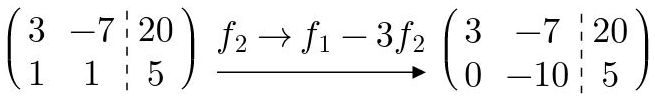
Fig. 21: Asignar a una fila una combinación lineal de filas (incluyendo a dicha fila la combinación lineal).
Nota: También es legal asignar una combinación lineal que no involucre la información de la fila a reemplazar pero existe el riesgo de perder información en el proceso.
-
Realizar una combinación de las operaciones anteriores de golpe
Para los impacientes. Hay que tener cuidado de no cometer errores!
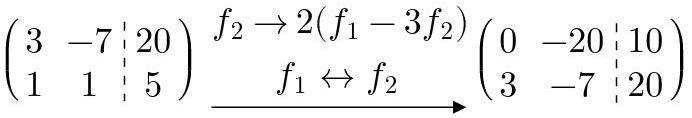
Fig. 22: Combinación de operaciones.
Las operaciones se realizan en cascada (de arriba hacia abajo).
Con las operaciones definidas anteriormente, una de las formas en las que se puede resolver el sistema de ecuaciones de la Fig. 14 es la siguiente:
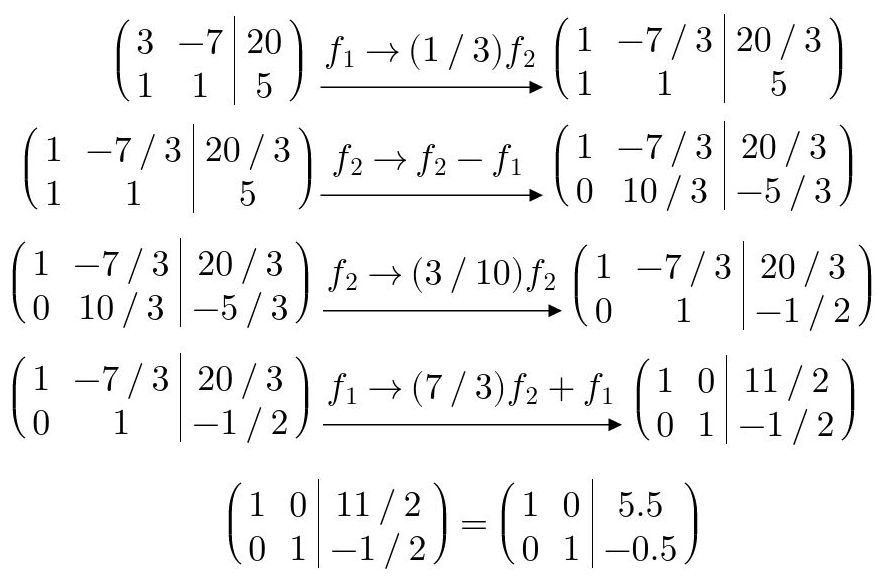
Fig. 23: Resolución del sistema de ecuaciones de la Fig. 14 a través del método de Gauss-Jordan.
Al realizar el proceso de reducción de Gauss-Jordan sobre una matriz extendida puede ocurrir una de las siguientes situaciones:
- Todos los coeficientes de una fila quedan igual a cero: La fila se eliminó por ser una combinación lineal de las demás filas
- La parte extendida de una fila es diferente de cero cuando todos los demás coeficientes son cero: El sistema de ecuaciones asociado no tiene solución.
- No se pueden despejar todas las incógnitas al final del proceso: El sistema de ecuaciones asociado posee infinitas soluciones.
Existe una teoría gigantesca de la relación entre sistemas de ecuaciones lineales y las matrices, para más ejemplos/problemas/información sobre este método puede consultarse en las referencias.
Matrices triangulares, diagonales y escalares
Las matrices triangulares son matrices que tienen ceros por arriba o por debajo de su diagonal principal. La diagonal principal empieza desde el elemento 11 y avanza diagonalmente hasta los límites de la matriz
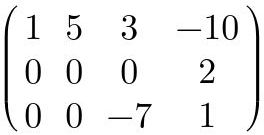
Fig. 24: Ejemplo de matriz triangular.
Las matrices tringulares pueden ser superiores o inferiores. Lo que esto quiere decir es el lugar en donde se encuentran los ceros. En el caso de la matriz triangular superior, los elementos debajo de la diagonal principal son cero, y en el caso de la matriz triangular inferior los elementos arriba de la diagonal principal son cero.
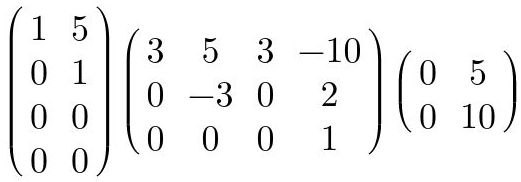
Fig. 25: Ejemplo de matriz triangular superior.
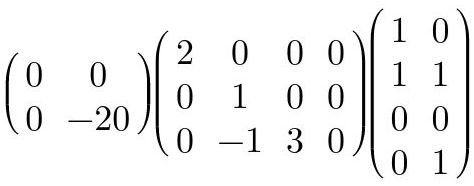
Fig. 26: Ejemplo de matriz triangular inferior.
Las matrices diagonales son matrices que tienen todos los elementos fuera de la diagonal principal igual a cero. Es una matriz triangular superior e inferior a la vez.

Fig. 27: Ejemplo de matriz diagonal.
Las matrices escalares son matrices diagonales en donde todos los elementos de la diagonal son iguales entre sí.
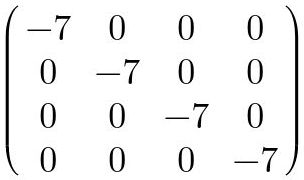
Fig. 28: Ejemplo de matriz escalar.
Una matriz completamente llena de ceros es una matriz triangular superior e inferior, diagonal y escalar a la vez. Este tipo de matriz se llama matriz cero.
Nota: En general, se refiere a las matrices triangulares, diagonales y escalares como subconjuntos de las matrices cuadradas pero en mi opinión creo que pueden ser o no ser cuadradas.
Matrices cuadradas
Las matrices cuadradas son matrices cuyas dimensiones horizontal y vertical son de igual magnitud. 1x1, 2x2, 3x3, 4x4, etc. son todas dimensiones de matrices cuadradas.
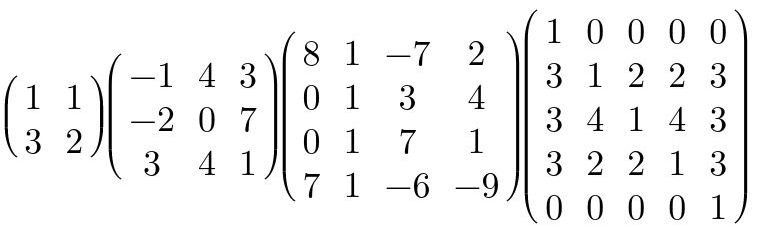
Fig. 29: Ejemplos de matrices cuadradas.
Las matrices cuadradas son el tipo de matriz más utilizada ya que siempre 2 matrices cuadradas de igual dimensión van a poder multiplicarse sin importar el orden en el que se pongan dichas matrices (la multiplicación no es commutativa!). También se usan ya que para ellas existen operaciones/propiedades para caracterizarla, como lo es el determinante y la matriz inversa.
Matrices unidad/identidad
Las matrices unidad/identidad son matrices diagonales cuyos elementos de la diagonal principal son todos 1. Estas matrices tienen la propiedad de multiplicar a cualquier otra matriz y no modificarla en el proceso. Esta matriz es el elemento neutro de la multiplicación y en general se le denota por I.
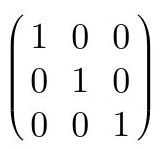
Fig. 30: Matriz identidad de 3x3.
De la seccion del método de Gauss-Jordan puede verse que al aplicar dicho método a una matriz extendida queda del lado izquierdo (si el sistema de ecuaciones asociado tiene solución única) una matriz identidad.
Menor complementario ij de una matriz.
El menor complementario ij de una matriz cuadrada es el determinante de la submatriz que se obtiene al eliminar la fila i y la columna j de la matriz original.
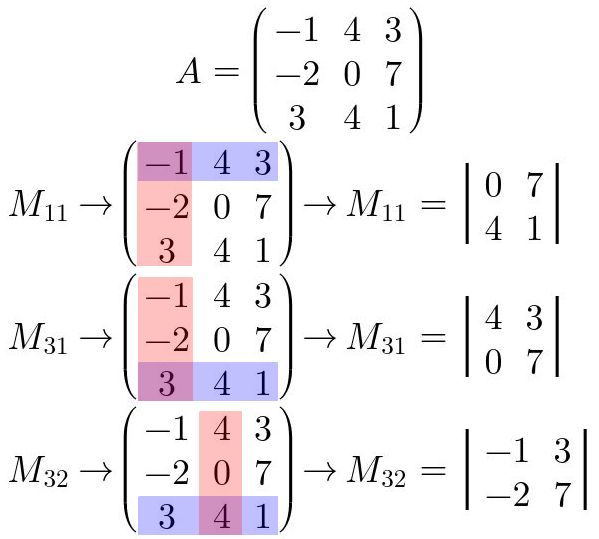
Fig. 31: Ejemplos del menor complementario ij de una matriz.
Cofactor ij de una matriz.
El cofactor ij de una matriz cuadrada es el Menor complementario ij de la misma matriz multiplicado por la potencia (-1)^(i + j).
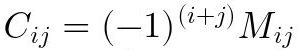
Fig. 32: Fórmula del cofactor ij de una matriz.
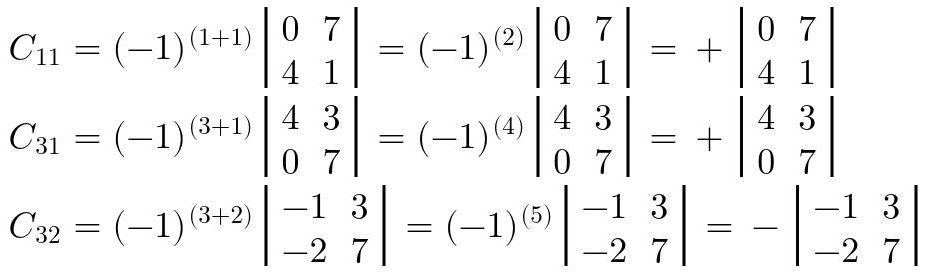
Fig. 33: Ejemplos del cofactor ij de la matriz de la Fig. 31.
Determinante de una matriz cuadrada
Las matrices cuadradas tienen una propiedad interesante que es el determinante. Este elemento es un escalar propio de la matriz cuyo valor númerico se puede usar para caracterizar la solución del sistema de ecuaciones asociado (con cualquier columna de extensión). De cierta forma se puede decir que "determina" las caracteristicas generales de la matriz.
El proceso de calculo del determinante de una matriz cuadrada es un proceso que se puede definir usando la definición del cofactor ij y considerando que el determinante de una matriz 1x1 es el valor numérico de su único elemento.
La descripción de este proceso no es sencilla ya que se puede escribir de diferentes formas. Se hará un ejemplo con una matriz de 2x2 y luego con una matriz de 3x3.
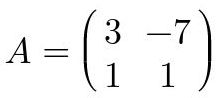
Fig. 34: Matriz ejemplo de 2x2.
-
El determinante tiene las siguientes representaciones, se puede usar cualquiera de ellas aunque en mi opinion la notación con las barras verticales es más fácil de recordar y aplicar para casos prácticos.
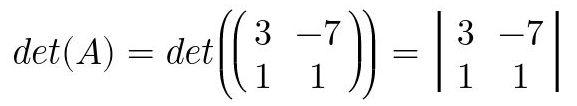
Fig. 35: Representaciones generales de un determinante.
-
Se selecciona una fila o columna a recorrer. Cualquier fila o columna. El recorrido puede ser en el sentido deseado. Voy a seleccionar la primera fila y la recorreré de izquierda a derecha.
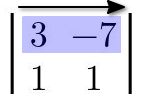
Fig. 36: Selección de la fila/columna a recorrer en la matriz
2x2ejemplo. -
Por cada elemento
1jde la fila se realiza el siguiente procedimiento: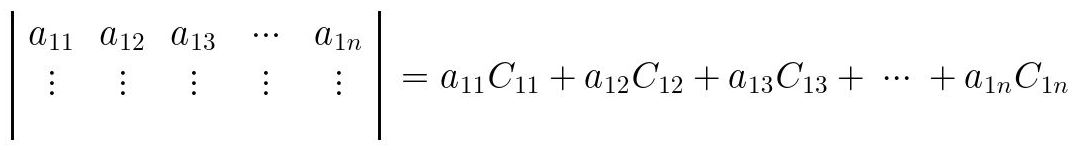
Fig. 37: Procedimiento de obtención del determinante de una matriz cuadrada genérica.
Que se traduce en la matriz ejemplo de
2x2como: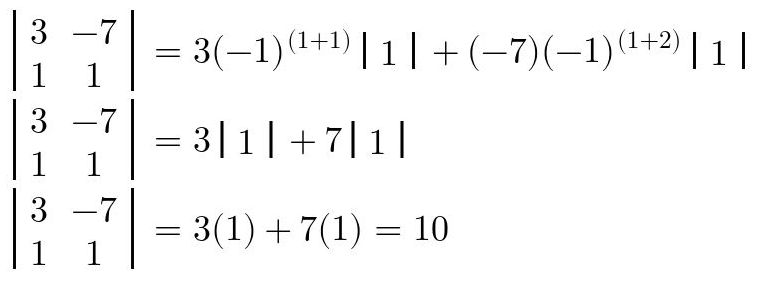
Fig. 38: Procedimiento de obtención del determinante de la matriz
2x2ejemplo.Puede recordarse el determinante de una matriz de
2x2de la siguiente forma más sencilla: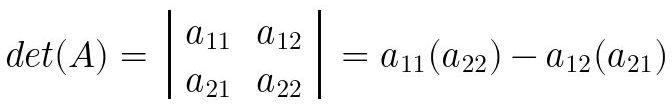
Fig. 39: Procedimiento de obtención del determinante de una matriz genérica de
2x2.
Para una matriz de 3x3:
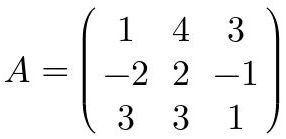
Fig. 40: Matriz ejemplo de 3x3.
-
Se selecciona una fila o columna a recorrer. Voy a seleccionar la tercera columna y la recorreré de abajo hacia arriba.
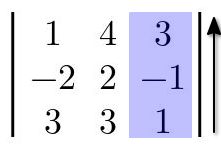
Fig. 41: Selección de la fila/columna a recorrer en la matriz
3x3ejemplo. -
Se realiza el procedimiento genérico mostrado en la Fig. 35 pero para la 3era columna de la matriz de
3x3: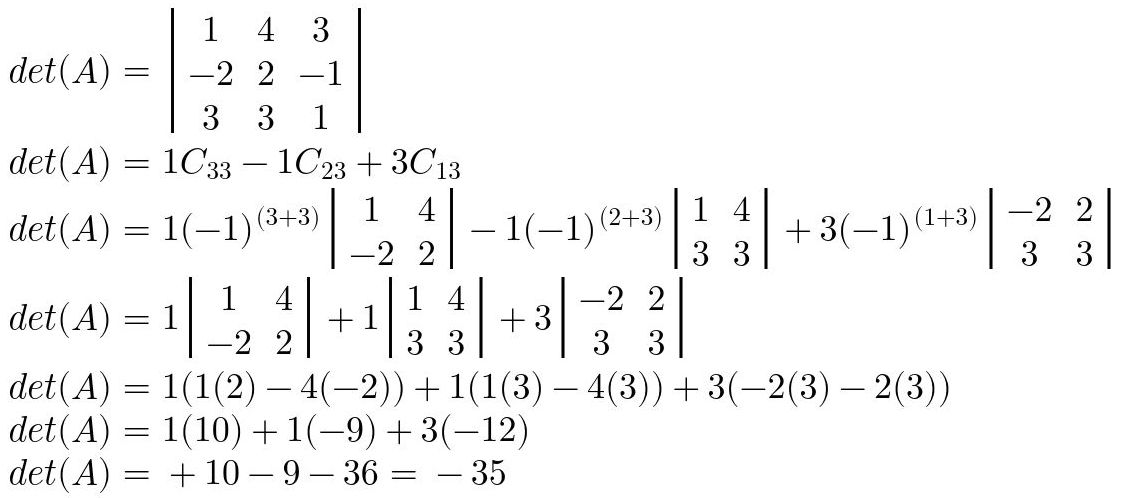
Fig. 42: Procedimiento de obtención del determinante de la matriz
3x3ejemplo.Puede recordarse el determinante de una matriz de
3x3de una forma más sencilla a través del Método de la Lluvia o Regla de Sarrus.
Para matrices de 4x4, hasta infinito... hay que trabajar >:]
Propiedades del determinante:
- Si el determinante de una matriz es distinto de 0 entonces el sistema de ecuaciones asociado tiene solución única.
- Si el determinante de una matriz es igual a 0 entonces el sistema de ecuaciones asociado tiene infinitas soluciones o no tiene solución.
Nota: hay una larga lista de otras propiedades que puede encontrarse en las referencias.
Se demuestra que el determinante de las matrices triangulares es el producto de los elementos de la diagonal principal.
Inversa de una matriz cuadrada
Otra característica interesante de las matrices cuadradas es la posibilidad de tener una inversa. La inversa tiene una gran importancia en transformaciones lineales por lo que es importante conocer como obtenerla y como saber si existe.
La condición más sencilla para probar si una matriz posee inversa es calculandole su determinante, si dicho determinante resulta en 0 entonces la matriz no posee inversa, de lo contrario, se puede determinar su inversa con los siguientes métodos.
-
A través del método de Gauss-Jordan
Se puede determinar una matriz inversa a través del método de eliminación de Gauss-Jordan extendiendo la matriz cuadrada a una matriz identidad de igual tamaño que la matriz a invertir. En el procedimiento lo que se busca es generar la matriz identidad del lado izquierdo, cuando dicha condición se satisfaga, lo que quede del lado derecho (la extensión) será la matriz inversa buscada.
Ejemplo: Hallar la inversa de la matriz
2x2de la Fig. 34: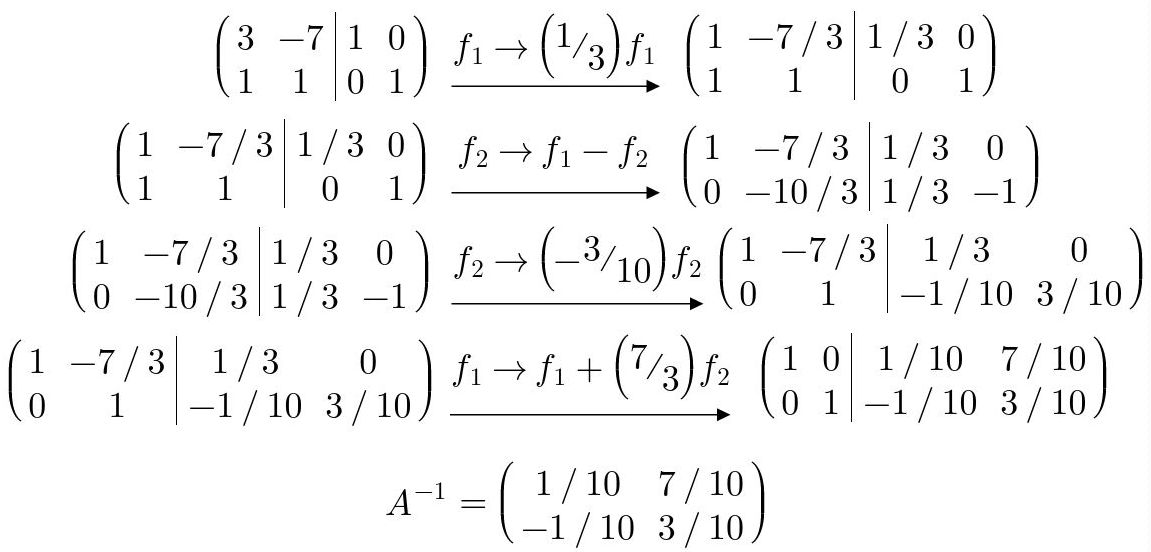
Fig. 43: Obtención de la matriz inversa de la matriz de la Fig. 34.
-
A través del determinante y la matriz adjunta
La matriz adjunta de una matriz cuadrada
Aes una matriz en la que sus elementosijson los cofactoresjide la matrizA.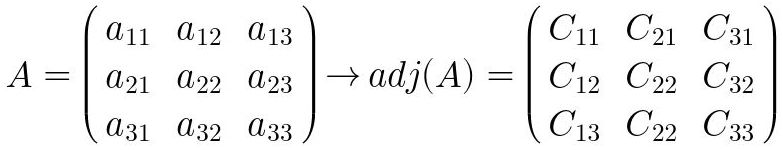
Fig. 44: Matriz adjunta de una matriz de
3x3.Con la matriz adjunta, la inversa de una matriz viene dada por:
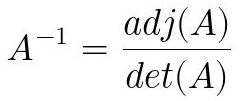
Fig. 45: Inversa de una matriz a través del determinante y la matriz adjunta.
Propiedades:
- Una matriz multiplicada por su inversa resulta en la matriz identidad sin importar el orden de la multiplicación.
- La inversa de una matriz es única, no hay 2 matrices inversas diferentes para una sola matriz.
- Una matriz cuadrada que no tenga inversa se le denomina matriz singular, es decir, está sola :,(
-
Si
Ces el producto de dos matrices invertiblesAyBcomo sigue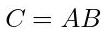
Fig. 46: Matriz
Cproducto deAyB.entonces la inversa de
Cexiste y viene dada por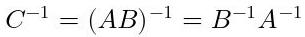
Fig. 47: Inversa de la matriz
Cde la Fig. 46.
Más teoría acerca de las matrices inversas puede conseguirse en las referencias.
Matrices ortogonales
Una matriz ortogonal es la matriz en la que su traspuesta es igual a su inversa.
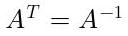
Fig. 48: Definición de matriz ortogonal.
Propiedades
- El determinante de una matriz ortogonal es
+1o-1. - El producto de matrices ortogonales es una matriz ortogonal.
- La inversa de una matriz ortogonal es una matriz ortogonal.
Referencias
- Álgebra Lineal, Stanley Grossman, 6ta edición
- Classical Mechanics, Volume 1, Edward A. Desloge
- https://es.wikipedia.org/wiki/Matriz_(matem%C3%A1tica)